Studiare le tabelline è una fatica per tutti, per alcuni un po’ di più e per altri un po’ di meno. In tutto il mondo, anche per i bambini cinesi.
(Ecco un metodo per imparare le tabelline in Cina.)

In questa pagina di SplashScuola trovate molte attività e giochi, in fondo alla pagina ci sono anche le canzoncine. Fra i giochi vi segnalo in particolare questo:

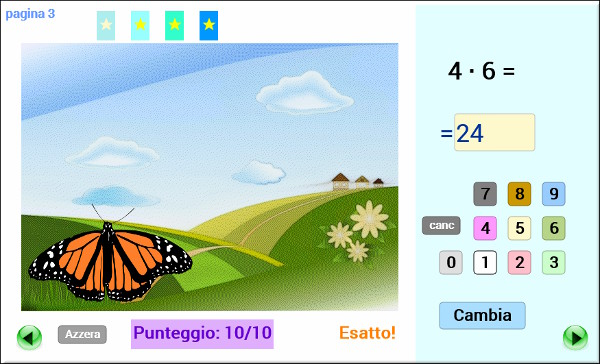
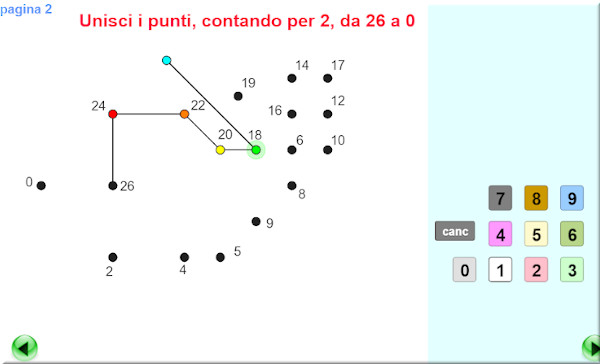
Ci sono più livelli di difficoltà e alla fine di ogni livello, dopo aver conquistato le stelle 🌟🌟🌟🌟🌟, il gioco unisci i punti (aspettate con pazienza dopo la conclusione del gioco).
Fate clic sul pulsante Cambia per una nuova moltiplicazione.

Buon divertimento!