[Filmato del 1936 da Wikipedia]
Non abbiamo proprio parlato di Braccio di Ferro–Popeye the Sailor Man, ma delle potenze dei numeri.
Un piccolo cenno.
Che cos’è dunque la potenza di un numero?
Possiamo immaginare la potenza come una scrittura abbreviata di una moltiplicazione con i fattori uguali.

32 = 3 • 3 = 9 (si legge tre alla seconda)
34 = 3 • 3 • 3 • 3 = 81 (si legge tre alla quarta)
53 = 5 • 5 • 5 = 125 (si legge cinque alla terza)
42 = 4 • 4 = 16 (si legge quattro alla seconda)
Siamo poi passati alle potenze di 10. Non vi dico lo sconcerto – vero Anna? – quando vi ho detto che dieci alla zero è uguale a uno e non vi ho ancora detto che… No no, taccio non ve ne parlo ancora.
100 = 1
101 = 10
102 = 10 • 10 = 100
103 = 10 • 10 • 10 = 1 000
104 = 10 • 10 • 10 • 10 = 10 000
105 = 10 • 10 • 10 • 10 • 10 = 100 000
106 = 10 • 10 • 10 • 10 • 10 • 10 = 1 000 000
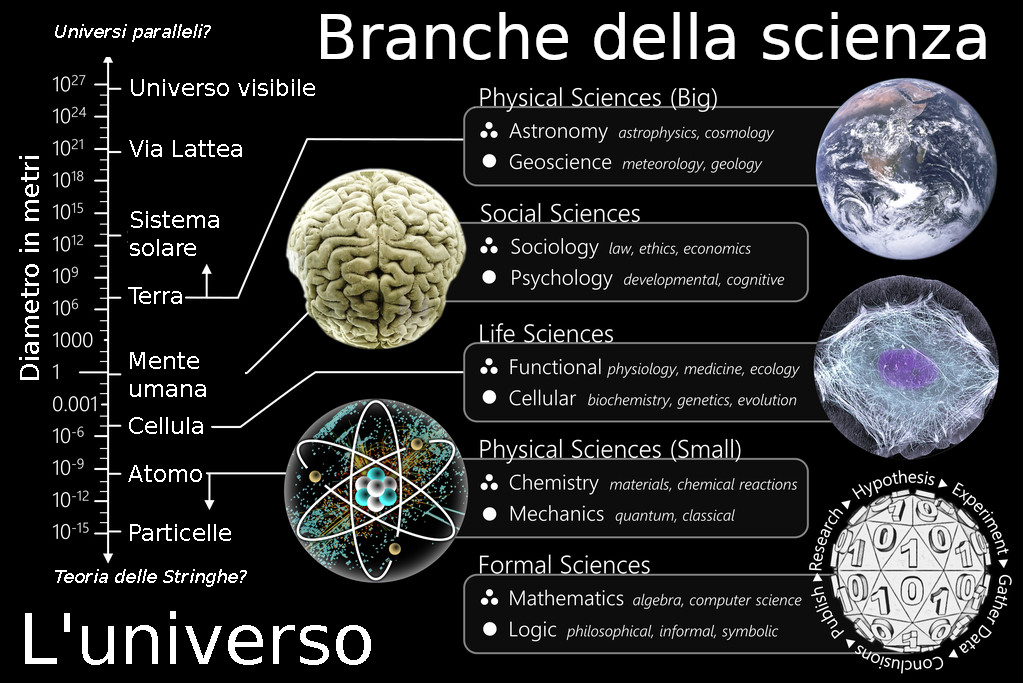
Perché dunque abbiamo trattato le potenze di 10? Volevo analizzare con voi questa immagine, immagine non semplice da capire, tratta da Wikipedia e parzialmente tradotta, sulle branche della scienza. Il numero 1 che leggete a sinistra corrisponde a 1 metro, 1000 metri sono 1 chilometro.
Rivedete, se lo desiderate, in Splash Ragazzi il bellissimo filmato (Powers of ten) che abbiamo visto a scuola, qui sotto in lingua inglese.
Come si dice alla fine del filmato (1977) le scoperte non sono finite, non si parla ancora di altre particelle subatomiche e noi certo non le tratteremo diffusamente, ma…
Occorre ringraziare Mattia che ha voluto portarci il libro che parla del bosone di Higgs, si veda Il sogno di una ballerina.

 Consiglio a chi di voi è più interessato due link che portano al blog del fisico italiano Marco Delmastro, in uno dei due link si segnala un libro «Particelle familiari: Le avventure della fisica e del bosone di Higgs, con Pulce al seguito». Chissà, magari ne riparliamo.
Consiglio a chi di voi è più interessato due link che portano al blog del fisico italiano Marco Delmastro, in uno dei due link si segnala un libro «Particelle familiari: Le avventure della fisica e del bosone di Higgs, con Pulce al seguito». Chissà, magari ne riparliamo.
⚛ Il bosone di Higgs spiegato a Oliver
⚛ Particelle familiari
 Oliver è un cagnolino. E Pulce chi sarà?
Oliver è un cagnolino. E Pulce chi sarà?
p. s. – il maialino inserito nel disegno che introduce alle potenze non è, per la nostra classe, casuale.
Link
• Potenze di dieci (video)
• Da un chicco di caffè a un atomo di carbonio
• The scale of the Universe
• Alla ricerca dell’infinitamente piccolo

 Anno scolastico 2004-2005: classe quarta
Anno scolastico 2004-2005: classe quarta