Cari bambini e care bambine, come preannunciato nelle nostre lezioni telematiche, vi presento un drago, un drago invisibile, che ci aiuterà con una nuova operazione, la sottrazione.
I draghi sono animali immaginari, se fate clic ne potete vedere uno in un disegno di circa duecento anni fa.
Torniamo al nostro drago. Alcuni video sono in inglese, non preoccupatevi, si capisce lo stesso la grande amicizia che c’è fra Pete ed Elliott, il drago invisibile.
Anche Elliott, come il coccodrillo Alan, è un gran mangione, eccolo:
Potete rivedere il video qui, un po’ più lungo.
Per chi lo desidera, la canzoncina in italiano:
Un’altra scena:




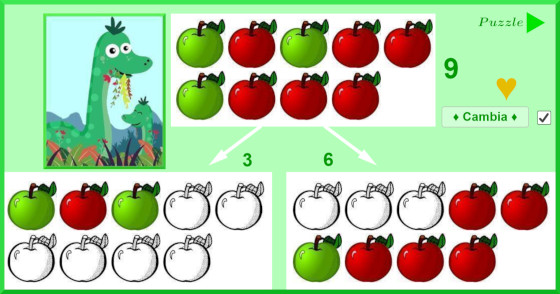

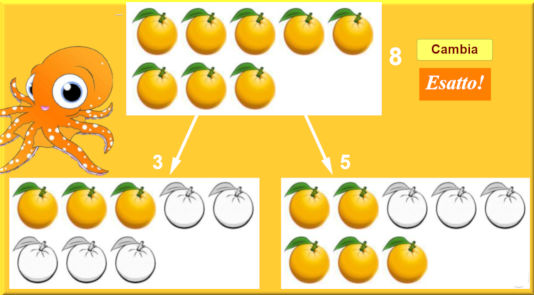
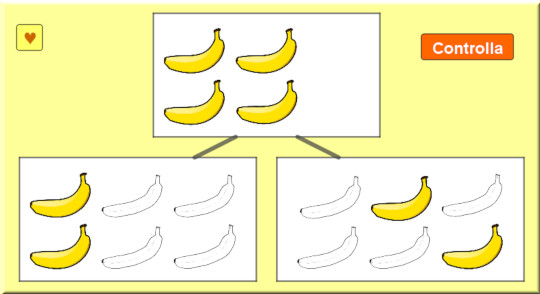
 Anno scolastico 2004-2005: classe quarta
Anno scolastico 2004-2005: classe quarta