Carissimi bambini e carissime bambine,
vi segnalo un mio vecchio tutorial con video che descrive come costruire un caleidoscopio con GeoGebra, che abbiamo già provato a fare in una delle lezioni estemporanee su GeoGebra. Il tutorial vi guiderà passo a passo mostrandovi come procedere.
Per visualizzare le diverse pagine del tutorial fate clic sul menu a sinistra, come vedete nell’immagine, oppure in basso a destra su Prossimo.
La versione di GeoGebra che troverete nel tutorial è datata, ma sicuramente siete in grado di orientarvi.
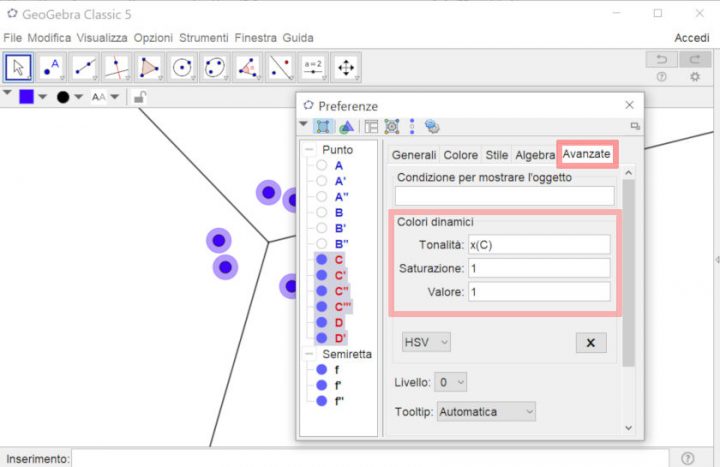
Una piccola aggiunta al tutorial, potete creare un punto con traccia arcobaleno usando l’opzione dei colori HVS invece che RGB, come vedete nell’immagine qui sotto.
Infine in questa pagina trovate dei caleidoscopio, realizzato assieme a Emanuele, uno con uno slider che visualizza punti con differenti effetti di colore e l’altro con fondo scuro.
Aspettatevi un’aggiunta a questa attività. A presto.
Anno scolastico 2004-2005: classe quarta