[Clic sui tre punti verticali per lo schermo intero]
Con i regoli
Reply
Tag Archives: geometria
Pavimentazioni
Divertiti anche tu con le pavimentazioni. Vai a questo sito: http://infinitefunspace.com/ptiler/
Chi lo desidera può mandare l’immagine della propria costruzione all’indirizzo mail della maestra (Centrare l’immagine con il bersaglio in basso a destra, tasto destro del mouse sull’immagine, scegliere nella finestra che si apre Salva immagine con nome).
Figure sui punti
Cari bambini e care bambine, dopo questa attività, eccovene un’altra.
Occorre costruire le FIGURE SUI PUNTI.
Clic sull’immagine per giocare.
Relazioni spaziali
Come sul quaderno: coloriamo il SERPENTELLO con GeoGebra. Anzi, non troverete un solo serpentello come sul quaderno, ma 2 serpentelli.
Clic sull’immagine.
Linee sui punti
Cari bambini e care bambine, abbiamo giocato un po’ a scuola con questa applet di GeoGebra.
So che volevate provare ancora a tracciare le LINEE SUI NOVE PUNTI.
Fate clic sull’immagine della scimmietta allora, chiedete a un adulto di leggervi le istruzioni e… BUON DIVERTIMENTO.
Happy Halloween
Un divertente HALLOWEEN ai cari bambini e alle care bambine di classe prima, con animazioni e due puzzle.
Halloween con Geogebra:
 |
Il ragno e la ragnatela |
 |
Il castello e i pipistrelli |
DUE PUZZLE
Clic su: primo puzzle, secondo puzzle.
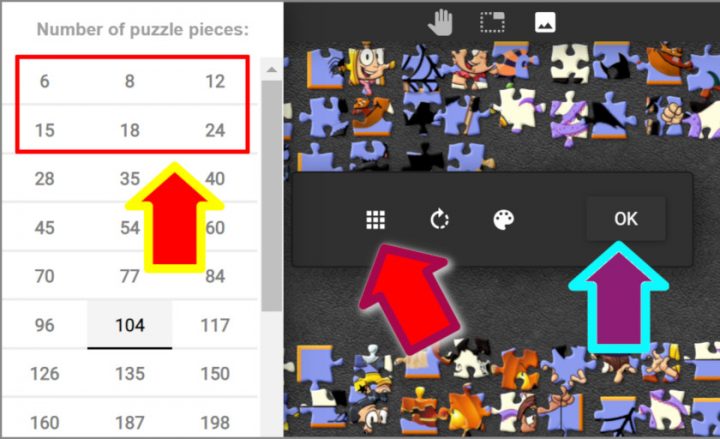
Quando si apre la pagina fate clic sui NOVE PUNTI per scegliere il NUMERO DI PEZZI del puzzle che preferite e poi su OK. Vedi IMMAGINE.
Per cambiare successivamente il numero dei pezzi clic in ALTO A SINISTRA su ☰.
In ALTO A DESTRA potete scegliere la visualizzazione a schermo intero.
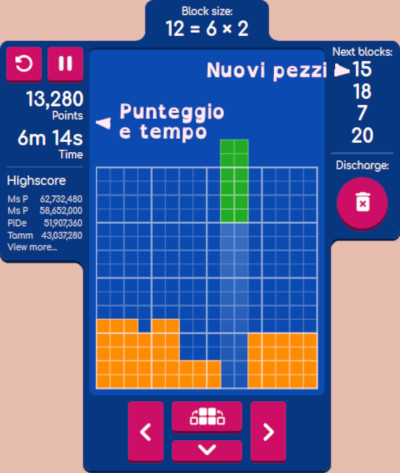
Non è Tetris ma Factris
Conoscete il gioco Tetris?
Fate clic sulla parola qui in alto e trovate alcuni articoli in Splash ragazzi che vi indicano dove poter giocare (c’è anche un tetris con gli stati europei).
I pezzi del tetris non sono altro che i tetramini, con rotazioni e riflessioni.
Vi segnalo un gioco che si ispira a Tetris, si chiama Factris (fattori e tetris). Per visualizzare il gioco e il punteggio provate a usare lo zoom, il tasto ctrl più il + o il – della tastiera. Si gioca con le frecce della tastiera o facendo clic con i pulsanti della shermata.
È un buon esercizio matematico. Provatelo e buon divertimento!
Tutorial: costruire un caleidoscopio con GeoGebra
Carissimi bambini e carissime bambine,
vi segnalo un mio vecchio tutorial con video che descrive come costruire un caleidoscopio con GeoGebra, che abbiamo già provato a fare in una delle lezioni estemporanee su GeoGebra. Il tutorial vi guiderà passo a passo mostrandovi come procedere.
Per visualizzare le diverse pagine del tutorial fate clic sul menu a sinistra, come vedete nell’immagine, oppure in basso a destra su Prossimo.
La versione di GeoGebra che troverete nel tutorial è datata, ma sicuramente siete in grado di orientarvi.
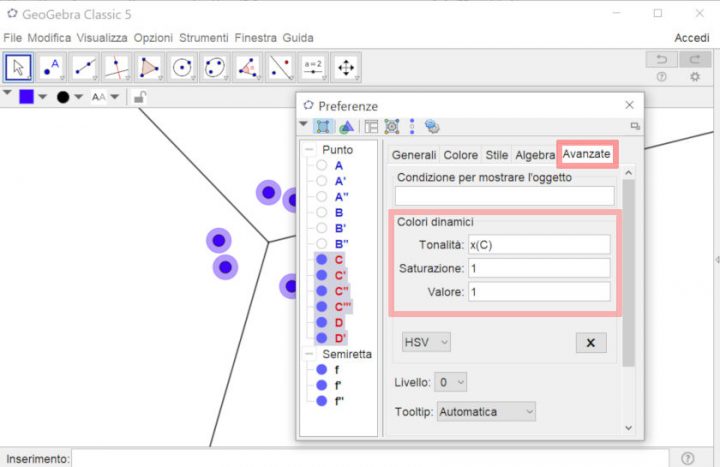
Una piccola aggiunta al tutorial, potete creare un punto con traccia arcobaleno usando l’opzione dei colori HVS invece che RGB, come vedete nell’immagine qui sotto.
Infine in questa pagina trovate dei caleidoscopio, realizzato assieme a Emanuele, uno con uno slider che visualizza punti con differenti effetti di colore e l’altro con fondo scuro.
Aspettatevi un’aggiunta a questa attività. A presto.
Anno scolastico 2004-2005: classe quarta