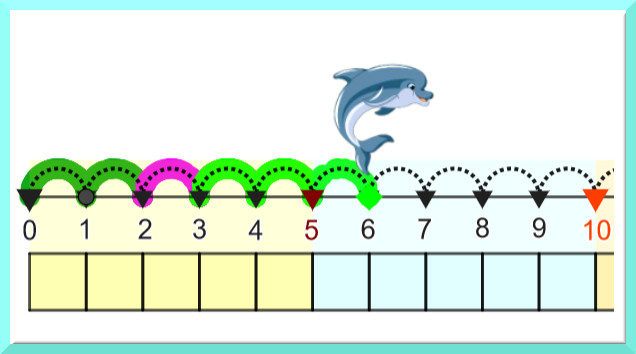
Addizioni e sottrazioni sulla linea dei numeri, fino al 25. Applet di GeoGebra in Splash Scuola.
Tag Archives: esercizi in splashscuola
A caccia dell’intruso
Se riesci a trovare tutti gli intrusi, comparirà un puzzle. Attività creata con GeoGebra. Fai clic sull’immagine qui sotto.

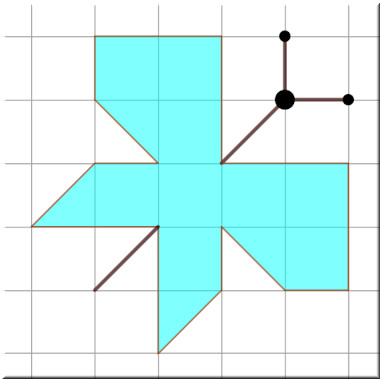
Simmetria di una farfalla
Ricomponete i pezzi per formare la farfalla. Alla fine piccole sorprese sui Lepidotteri: farfalle e falene.
Fare clic sull’immagine.
🦋 Link per i tanti bambini e le tante bambine che amano i piccoli animali:
• Galleria di video di Gianluca Doremi
• Tutto sulle farfalle e le falene
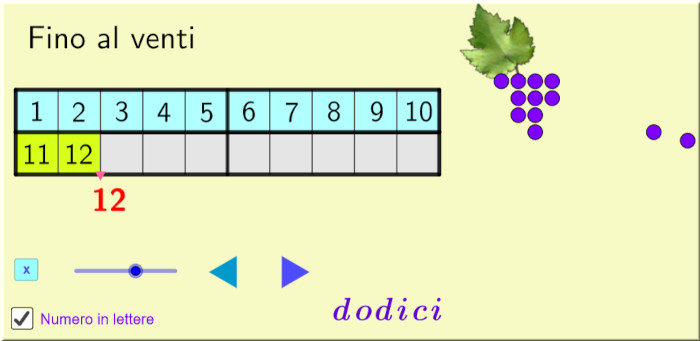
Numeri fino al venti
Numeri, disegni e parole
La scheda di italiano della maestra Silvana che avete completato ieri conteneva alcune cose curiose.
C’era un ago e un mago, c’era una gabbia e un gabbiano…
Ecco allora l’occasione per parlare di REBUS!
 Clic sui collegamenti:
Clic sui collegamenti:
👑 🚌 Che cos’è un rebus?
💙 Rebus e numeri (5 pagine)
💙 Altri rebus (e scrittura di parole)
💙 Un’altra lavagna di rebus
Formare il nove
Esercizio sul numero nove con gli uccelli acquatici.
Applet di GeoGebra. Fai clic sull’immagine qui sotto.

Numeri entro il nove
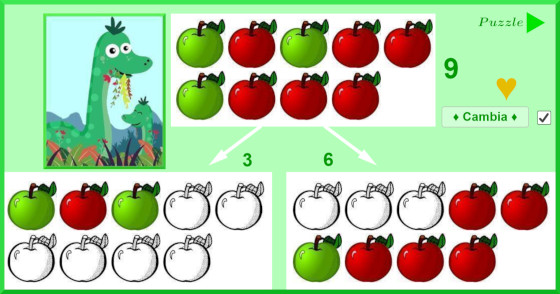
Esercizio con i numeri fino al nove con le mele, con puzzle da ricostruire.
🍎 🍏 🍎 🍏 🍎 🍏 🍎 🍏 🍎
Clic sull’immagine.
Introduzione al numero 9
Aggiorniamo il blog e il sito con le ultime attività con cui abbiamo lavorato (e giocato) a scuola.
Introduzione al numero 9 con un’applet di GeoGebra.


 Anno scolastico 2004-2005: classe quarta
Anno scolastico 2004-2005: classe quarta